今回は、「2_2_複素数と方程式」を振り返っていきます。ここのあたりから一気に苦手意識をもって脱落していく人が増えていくのではないでしょうか。
難しく考えすぎず、分かるところまで理解できたらいいやっていう軽い気持ちで取り組んでみてください。やっている内になんとなく理解が進んでいくはずです。
- 概要
- 考察
- 2-2-1 複素数
- 2-2-1-1 虚数の考え方
- 2-2-1-2 複素数
- 2-2-1-3 共役な複素数
- 2-2-1-4 複素数の計算
- 2-2-2 2次方程式の解と判別式
- 2-2-2-1 2次方程式の解の公式
- 2-2-2-2 判別式
- 2-2-3 解と係数の関係, 解の存在範囲
- 2-2-3-1 解と係数の関係
- 2-2-3-2 2次方程式の解の位置と条件
- 2-2-4 剰余の定理と因数定理
- 2-2-4-1 剰余の定理
- 2-2-4-2 因数定理
- 2-2-4-3 組み立て除法
- 2-2-5 高次方程式
- 2-2-5-1 高次方程式の解法
- 2-2-5-2 3次方程式の解と係数の関係
- 2-2-1 複素数
- まとめ
概要
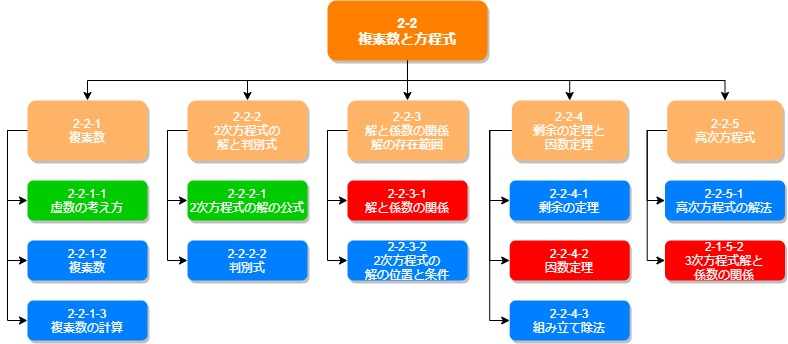
この分野は、「複素数」と「方程式」の二つに分かれます。
複素数については少しとっつきにくい感覚を持っている受験生も多いかもしれませんが、難しく考えず、2乗したら-1になるiっていう文字が加わった数字だなレベルくらいの理解で十分解答できます。
円周率を表す文字πが加わった数字として、2πなどを考えるのと大きな違いはありません。πを文字として扱うのと同じように、iも文字として扱って処理していく。iにはどのような性質があるのかだけ押さえておけば問題ありません。
方程式については、1-3 二次関数でやったところをしっかり押さえておけば問題ありません。高次方程式も、1次方程式と2次方程式に分解して考えていくしかありません。受験生が解くことができるのは2次方程式までです。3次以上の方程式が表れた時は、どうにかして2次以下に分解しないと解くことはできない。分解できないのであればどこかで間違っているはずです。2次までしか自分にはとけないのだということをしっかり頭に入れておきましょう。
2-2-1では複素数の考え方、iの性質を学習します。このiを用いることで今まで以上に様々な二次方程式を解けるようになります。しっかりと押さえておきましょう。
2-2-2では2次方程式の解と判別式を学習しますが、ここはすでに1-3 二次関数で学習しています。なので、難しいところではありません。
確認しておきますが、判別式などは覚える必要はありません。平方完成を正しく行って、グラフを書くことができれば公式を知らなくても解答することができます。
2-2-3でも二次方程式について学習します。解の位置と条件の関係についても、グラフを正しく書ければ解答することができるので、覚えなくて大丈夫です。しかし、解と係数の関係については非常に便利な公式なので覚えておきましょう。
どこを覚えて、どこを覚えないのか、しっかり全体のブロック図を見て重要度と照らし合わせながら確認しておきましょう。
2-2-4では剰余の定理・因数定理・組み立て除法を学習します。特に大切なのは、因数定理と組み立て除法です。因数定理を知らないと解けない問題が多々あるので、しっかり確認しておきましょう。また、組み立て除法を知っていると格段に解答スピードが上昇するので、押さえておきましょう。
2-2-5では高次方程式を扱います。上で述べたように、以下に2次以下に落とし込んでいくかだけがポイントです。自分が2次以上の方程式を解くことができないんだということを自覚して、その上でどのようにして2次以下に分解していくのかを学習していけるといいでしょう。
考察
2-2-1 複素数
2-2-1-1 虚数の考え方
虚数iの扱いを確認しておきましょう。これを知らないとどうしようもないので、しっかり押さえておいてください。
1, √(-1) = i
2, i2 = -1
3, i-1 = -i
2-2-1-2 複素数
複素数では、上で説明したiという文字が出てくる数字の概念になります。
複素数は実数と虚数からなり、文字式と同じように以下の性質を持ちます。
複素数:a+biについて、
b=0の時、これを実数という。
b≠0の時、これを虚数という。
特に、a=0かつb≠0の時、これを純虚数という。
複素数の性質:a+bi = c+diの時、a=c, b=dが成り立つ。
2-2-1-3 共役な複素数
a+biとa-biを、互いに共役な複素数という。
互いに共役な複素数の積は次数になる。( (a+bi)(a-bi) = a2+b2 )
2-2-1-4 複素数の計算
複素数の計算は、iを文字として扱うことで、これまでの文字式の計算と同様に行うことができます。そこに、iの性質を考慮することになります。
難しいところではないので、演習の中で理解しておきましょう。
2-2-2 2次方程式の解と判別式
2-2-2-1 2次方程式の解の公式
2次方程式は1-3 二次関数で学んだ通り、以下のようになります。
複素数という概念を学んだことで、√の中が負の数になった時についても、iによって説明することができるようになりました。√の中が負の数になる時、グラフを書いてもx軸とは交わらないので、変な感じがしますが、複素数の世界では交わっていると考えます。
ax2+bx+c = 0 (a≠0)の二次関数について、解は以下のように定まる
x = { -b±√(b2-4ac) } / 2a
2-2-2-2 判別式
以前にも述べたように、判別式は覚える必要はありません。
グラフを描いてみて、x軸と交わるところが存在するかどうか、交わるためにはどのような条件が必要なのか、頂点のy座標について考えるといいでしょう。
2-2-3 解と係数の関係, 解の存在範囲
2-2-3-1 解と係数の関係
解と係数の関係は覚えておきましょう。解の公式から導くことができますが、わざわざ考えるのは効率が悪いので、しっかり暗記しておくといいでしょう。難関校では、当然のように使えないといけない公式になります。解と係数の関係の逆の考え方も注意が必要です。
ax2+bx+c = 0 (a≠0)の2解がα, βである時、
α+β = -b/a
αβ = c/a
と表すことができます。
2-2-3-2 2次方程式の解の位置と条件
2-3 二次関数のところでも解の正負によって場合分けを行ったと思いますが、ここではさらに細かく場合分けを行って、それが成り立つための条件を考えていきます。難しく考える必要はなく、グラフを描いて大切なポイントの条件を書き出していけば、導いていくことができます。
演習を重ねながら理解を深めていきましょう。
2-2-4 剰余の定理と因数定理
2-2-4-1 剰余の定理
高次式P(x)を一次式(x-a)で割った時の余りは、P(a)で表される。
これが剰余の定理になります。簡単に確認しておきましょう。
特に、余りP(a)が0になる時は因数定理と呼ばれます。
因数定理は非常に大切な考え方なので、しっかり確認しておきましょう。
2-2-4-2 因数定理
一次式(x-a)が高次式P(x)の因数である ⇔ P(a) = 0
つまり、P(a) = 0の時、P(x) = (x-a)P'(x)と書き換えることができる。
高次式の問題では、因数定理を使って、次数の小さい因数に分解していくのが非常に大切になってきます。しっかり確認しておきましょう。
因数定理を用いて、P(a) = 0となる数aを見つけるためのポイントは、定数項の素因数を考えることがポイントです。これも合わせて覚えておきましょう。
2-2-4-3 組み立て除法
組み立て除法は整式の割り算を早くするための手法です。説明が難しいのでここでは割愛しますが、これは押さえておきましょう。問題を解くスピードに圧倒的な差がついてきてしまいます。
2-2-5 高次方程式
2-2-5-1 高次方程式の解法
2-2-4-2で説明した因数定理を用いて高次方程式は解いていきます。因数定理を用いて、2次以下の因数に分解して、それぞれの因数について考えることで解いていくことができます。
何度も言いますが、高次方程式を解く上で大切なことは、3次以上の方程式を解くことができないということを自覚することです。高次方程式で考えないといけないのは、いかに低次の方程式に分解するかという所です。分解ができなければどこかを間違っているはずです。
2-1-5-2 3次方程式の解と係数の関係
3次方程式の解の公式も覚えておきましょう。
ax3+bx2+cx+d = 0 (a≠0)の3解をα, β, γとすると、
α+β+γ = -b/a
αβ+βγ+γα = c/a
αβγ = -d/a
となる。
まとめ
今回は、「複素数と方程式」を振り返りました。
基本的には、2-3 二次関数で学習した内容の発展です。
グラフを描くことを大切にして下さい。小手先のテクニックに頼っていてはいけません。まずは、何が小手先のテクニックなのかを考えながら、演習を進めて、解答を読んでみましょう。
また、高次方程式を解く上で大切なのは、二次以下の方程式しか自分には解くことができないということを把握することだ、と何度も述べてきました。これは、この分野に限らず、様々な場面において大切な考え方です。
自分には何ができて、何ができないのか。だから、問題解決のためには何をしていかないといけないのか。順を追って考えていけるといいでしょう。受験勉強全体において、自分がどこが得意で、どこが苦手なのかを把握し、合格のためにはどうしていかないといけないのか。受験全体を俯瞰しして、何をすべきなのか論理的に考えていけるようになりましょう。
論理的に考えていくためにも、まず初めに自分をしっかり把握するというのは非常に大切です。演習をこなしていくよりも前に、自分の現状の分析、目標の設定をしてみてはいかがでしょうか。


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1a1cd25e.24151616.1a1cd25f.d286440e/?me_id=1251035&item_id=18142213&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fhmvjapan%2Fcabinet%2Fa03%2F86000%2F10384570.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fhmvjapan%2Fcabinet%2Fa03%2F86000%2F10384570.jpg%3F_ex%3D128x128&s=128x128&t=picttext)



