830の数学_2_6_微分法

今回は「微分法」を振り返っていきます。
苦手な意識を持っている人が非常に多い分野ではないでしょうか。しかし、覚えないといけないことは意外と少ない分野です。しっかりと処理方法を確認しておけば、案外難しくありません。導関数を求めて、増減表を書いて、グラフを描くことができれば、ほとんどの問題を解くことができます。
苦手意識は一回取っ払って、見直してみましょう。

チャート式 基礎からの数学II+B / チャート研究所 【本】 価格：2365円（税込、送料別) (2020/4/16時点)

概要

「微分法」では、まず平均変化率や微分係数の定義から勉強していきます。しかし、微分係数の定義などが非常に難しいので、多くの人はこの段階で、「微分法ムズカシー」ってなってしまうように感じます。しかし、難しいのは微分係数の定義のとこらへんだけで、グラフを描いたりするのは難しくありません。とりあえず、初めは微分係数の定義は飛ばして勉強していくといいのではないでしょうか。

2-6-1では微分係数の定義などを学んでいきます。ここが少し複雑で、もう無理ってなってしまう人が多いのではないでしょうか。まず初めはこの項を軽く流して勉強を進めていくことをおすすめします。導関数というものが接線の傾きを表すものであるというくらいだけ把握しておけば問題を解くには十分です。

2-6-2では接線と法線の表し方を学んでいきます。直線を書く時必要になるのは、直線の通る点と直線の角度の2つです。直線の通る点は接点であり、直線の角度は導関数を用いて求めることができます。この2つに着目しながら問題を解いていってみましょう。

2-6-3では増減表の書き方を勉強します。増減表を通して、極大・極小を考えていきます。導関数f'(x)の正負がグラフの増減を表しているということをしっかり確認しておきましょう。

2-6-4ではグラフの描き方を勉強します。増減表を通して、どのようにグラフを描いていくのかしっかり確認しておきましょう。方程式の実数解の個数や不等式の証明問題も出てきますが、いずれもしっかりとグラフを描くことができれば難しい問題ではありません。グラフの描き方をしっかり確認しておきましょう。

2-6-5では発展問題も紹介されているので確認しておきましょう。

考察

2-6-1 微分係数と導関数

2-6-1-1 平均変化率と微分係数

平均変化率は以下のように定義されます。平均変化率は言葉のままなので、理解しやすいのではないでしょうか。

次に、微分係数を考えます。微分係数と言われると難しく感じますが、微分係数とは曲線上のある点における接線の傾きを表しています。上の平均変化率の考え方において、bを限りなくaに近づけていけば、x=aにおける接線の傾きになるようなイメージ湧きませんかね。このbをaに近づけていくという作業を式で表す時に、limというものを使って表現します。

2-6-1-2 導関数

導関数は曲線上の点x=xにおける接線の傾きを求めるための関数です。ここにxの値を代入することで、その点における微分係数(接線の傾き)を求めることができます。導関数は上の微分係数の定義においてaをxに書き換えることで導くことができます。
平均変化率→微分係数→導関数という流れを押さえられると理解が深まるのではないでしょうか。

2-6-1-3 xⁿの微分

全ての関数f(x)の導関数は上記の導関数の定義から導くことができますが、数Ⅱの微分法の分野ではy=xⁿ上の微分しか問われないので、この導関数だけ覚えておけば十分です。ただし、定数項（n=0の時）には注意が必要です。

2-6-1-4 導関数の性質

導関数の計算に際して、以下のような性質があるので確認しておきましょう。

2-6-2 接線

2-6-2-1 接線の方程式

接線の方程式は以下のように求めることができる。
2-3 図形と方程式で学んだ直線の方程式の導出を見直してみましょう。
直線は、通る一点と直線の傾きが決まれば一意に定まり、方程式を導くことができます。

2-6-2-2 法線の方程式

法線の方程式についても以下のように求めることができる。
法線を考える時は、法線の傾きが重要になりますが、これも2-3 図形と方程式で学んだ2直線の垂直の考え方を用いると傾きを求めることができます。

2-6-3 関数の増減と極大・極小

2-6-3-1 関数の増減

関数f(x)の増減は導関数f'(x)の正負によって考える時ができます。

2-6-3-2 関数の極大・極小

極大・極小とは、局所的に最大・最小となっていることを表しています。つまり、極大点ではf'(x)が正→負、極小点ではf'(x)が負→正と変化していることになります。導関数の正負の転換点が極大点・極小点となります。これを見つけるために増減表を書きます。増減表を書くことで関数y=f(x)の概形を考えることができます。

説明が難しいのでここでは割愛しますが、x・f'(x)・f(x)それぞれに着目して増減表を書いていくことになります。

2-6-4 最大値・最小値、方程式・不等式

2-6-4-1 関数の最大値・最小値

増減表を元にグラフを描いて最大値・最小値を見つけていきます。しっかりと増減表をかけていれば、迷うことなくグラフを描くことができるでしょう。

また、三次関数では対称性が非常に重要になります。三次関数の対称性の考え方を理解していれば、解答のスピードは格段に速くなると思うので確認しておきましょう。

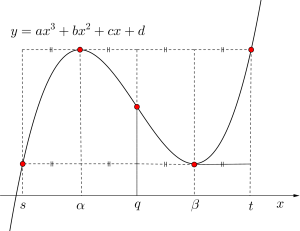
三次関数については、このグラフの対称性を利用してグラフを描くときれいに、さらに素早くグラフを描くことができます。まず初めに図のような長方形4つを書いてから、その中を埋めるように三次関数を描いていくといいでしょう。

2-6-4-2 方程式の実数解の個数

方程式の実数解の個数というのは、関数とx軸の交点の数を表しています。なので、グラフを描いてx軸との関係を考えていくことになります。
関数の中に変数が入ってくると、変数の値によってグラフの形が変化するため、x軸との関係も変わってきてしまいます。変数の値によって、x軸との交点の数がどのように変化するのかを考えていくことになります。こういった問題を考える時、グラフを書き換えたりするのではなく、グラフの概形に対してx軸の位置がどのように変化するのか、x軸を動かした方がいいでしょう。そちらの方が手間を少なく問題を解いていくことができるでしょう。
イメージしづらいかもしれませんが、演習を重ねながら理解を深めていきましょう。

2-6-4-3 不等式の証明

f(x)>g(x)のような不等式を考える場合は、f(x)-g(x)>0と式変形し、y=f(x)-g(x)のグラフを考えていくことになります。グラフを書くことができれば、x軸との位置関係を考えるだけなので、方程式と同様に考えていくことができるでしょう。

こちらも初めはややこしいかもしれませんが、演習をこなしている内に理解が深まっていくのではないでしょうか。

2-6-5 関連発展問題

まとめ

数Ⅱの微分は正直とても簡単です。
①導関数を求める→②増減表を書く→③グラフを描く→④グラフと条件を考える
ほとんどの問題はこの4ステップから解答することができます。自分はどこでつまづいているのかしっかり把握できるといいでしょう。
また、どこで時間がかかってしまっているのかという点も意識できるといいでしょう。三次関数のグラフを描くときに、対称性を知っているかなどによって大きくスピードが変わってきてしまいます。また、先にx軸・y軸を描くというのもNGです。圧倒的にスピードが落ちます。1-3 二次関数のところでも説明したように、グラフの概形を先に描いてから、後でx軸・y軸を書き込む。これがおすすめです。
微分は評判以上に簡単です。計算が煩雑になることはありますが、大変なのと難しいのでは話が違います。苦手意識を捨てて、簡単だって自分に思い込ませながら取り組んでいけるといいでしょう。